On AI sketch vectorization: Understanding and drawing Bézier curves

I'm reading through Virtual Sketching's paper.¹ Specifically, I've read the part about the quadratic Bézier curves used by the model to further understand what the model is learning. I'm slowly preparing a lecture on machine learning-based sketch vectorization, and for that, I want to thoroughly understand how this model works.

Googling, I came across a site² which talks in detail about Bézier curves in the context of CSS and web animation and referenced diagrams from Live 65's slides. A curve with two control points (or three control points that all lie in the same line) is a line. A Bézier curve with three control points is a quadratic curve. And a Bézier curve with four control points is a cubic curve.

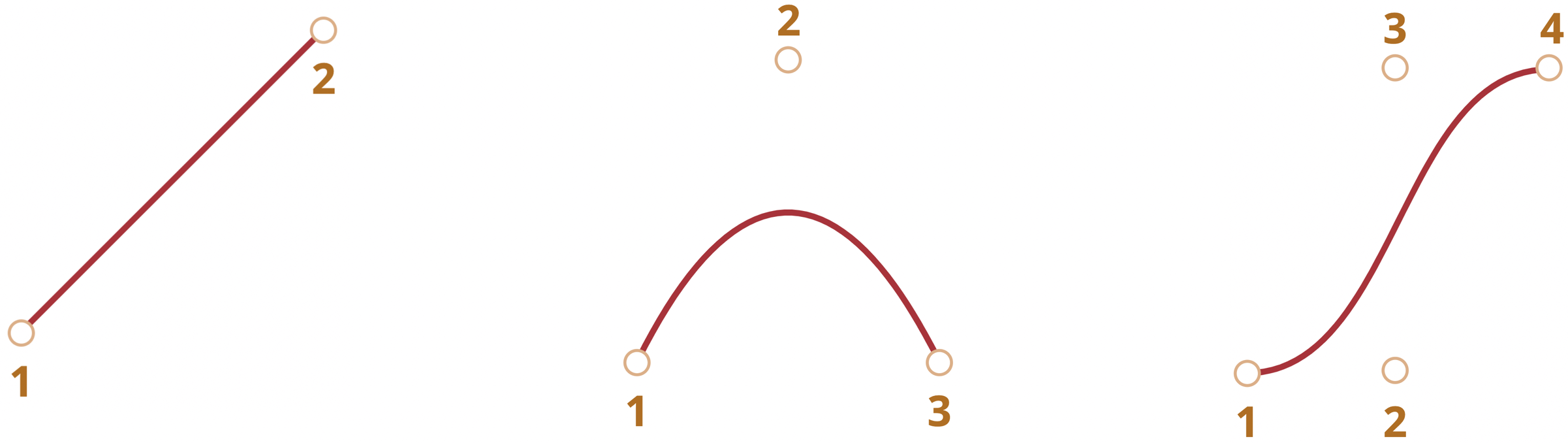
The paper uses curves with three control points, so it follows the following formula to render curves.

P(t) = (1−t)²P₁ + 2(1−t)tP₂ + t²P₃ with t ∈ [0, 1]

The cited page uses De Casteljau’s algorithm to build 3-point Bézier curves, and shows how curves with more control points can be built using interpolation.²

Take a look at yesterday's post for coding examples to draw quadratic Bézier curves.